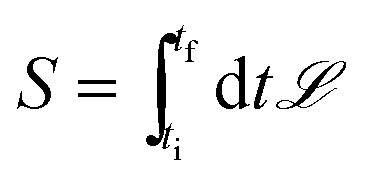티스토리 뷰
I. 기본 지식 ( 사전 지식)
A. 물리는 ? (적어도 이 시간에는) : 물체의 위치를 예언하는거.
예) a. 1년뒤에 달의 위치는 어디인가?
b. 1초뒤에 전자는 어디에서 찾을수 있을까?
B. 예언은 운동방적식이 해결
예) a. 뉴튼의 F=ma ----> 달이1년뒤 어딨는지 정확히 이야기해준다
b. 슈레딩거 방정식 ....> 전자가 1초뒤에 어디 있는지 확률적으로 알려준다.
C. 운동 방정식은 물체의 액숀(action ;S ) 과 라드랑지안(lagrangian;L) 이 해결 ;몰라도 됨
II. Path Integral
고전 역학 과 양자역학적 관점
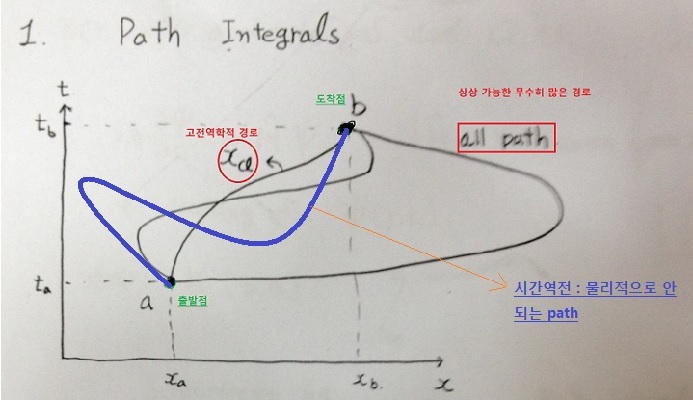
A. 아래 대략적 그림 ( 내 노트) : 이해/계산 하기쉽게 2차원 ( x, t) 쓰자 ; 그림만 이해 하자
출발점 a: ( xa , ta ) -> 도착점 b :( xb , tb )
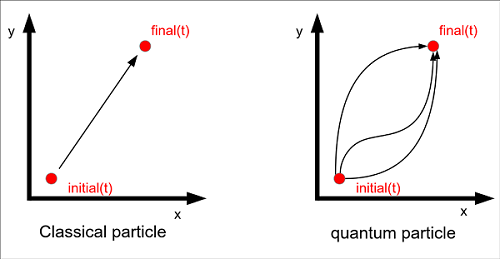
고전적 경로 : only Xcl
양자역학적 경로 : 모든 경로 (all path) 고려 ,; 단, 시간이 거꾸로가는 경로는 물리적으로 ㄴㄴ
모든 경로( all path ) 를 다 더해주면 ( = integral) 해주면 ,
입자가 나중에 어디에 있을지 확률적으로 알수있다.
그런데 가능한 경로의 수는 실제론 무한대이다 .
궁금하면 종이에다가 a, b 두개 점찍고 직접그려바라 실제로 몇개 나오나
이걸 어떻게 다 더하나? ㅅㅂ , 걱정마라 수학이 무한히 가능한 경로를 다 더해주게끔 도와준다.
실제론 패쑤인터그랄에서 해야할것은
1. S (액숀 ; action ) 구하기
2. S를 넣어서 적분하기
3. 그러면 그게 kernel; K (커널) 이다.
4. 커널을 절대치제곱(= 확룰) 하면 이제 입자가 어디에 있는지 확률적으로 예측할수 있다. 끝
III. free-particle 에 패쑤인테그랄을 적용 , 실제로 kernel을 구해보자
이 경우는 포텐샬이 없어서 제일 간단한 입자의 운동이야 , 예를 들면 중력( 포텐샬) 을 고려하지 않고 움직이는....
실제계산은 다음과 같고, 알필요도 없으며, 혹시 궁금한 게이는 답글달면 디테일하게 따로 올려줄께
우리는 다음과 같은 결과를 얻을수 있지
kernel
이게 우리가 원하는 free particle 의 커넬, K(a,b), 되시겠다.
Scl 은 클래시컬 액숀 (classical action) 임.
자, 이제, 이 K(a,b)로 one-slit에 적용해보자.
음..... 내가 머하는 짓인지 모르겠다
IV. 단일 슬릿 : one-slit
1. 고전 역학적 해석 ; 그림만 이해해라....
하지만 뚫린 구멍을 통과하는 양자역학적 가능한 경로를 생각하보면 이렇다
자 위에 그림에서 보듯이, 입자는 일게이 처럼 어디에든 있을수 있다.
거의 다왔다 게이들아 좀만 힘내보자.
엑기스만 다시 정리해보면 다음과 같다.
그래서 위에 빨간 박스안을 계산해주면 ,
마침내, 우리가 원하는 단일슬릿 회절 을 패쑤인테그랄로 표현했다
k2 와 k1 에다 실제로 구한 k 값을 넣어서 적분해주면 된다. 연습장에 하던지 , 프로그램 쓰던지 하면 쉽다.
VI. 결과
적분 결과는 뚜둥~~~
위짤은 적분한 결과 이다.
C, 와 S는 Fresnel Integral : 프랑스 수학자 이름일꺼임 구글링해보길 바란다
P(x) : 구멍 통과한 입자가 위치 x 에서 발견될 확률
위에 식에 적당한 질량(m) , 속도(v0), 구멍 크기(b) 등등을 넣어서 그림을 구려주면
구멍크기(b) 변화에 따른 회절
이렇게 회절 무뉘를 볼수있게다
예를 들어 그래프가 높은쪽은 입자를 발견할 확률이 높은거고
낮은쪽은 발견할 확률이 낮은거다..
혹시 더 궁금하면 내 노트도 올려놀께 거의 디테일하게 계산해놨다. 책 연습문제도 헤헤
요약
1. 파인만의 경로적분 (path integral ) 은 양자역학의 또다른 접근법
2. 이걸로 전자혹은 작은입자의 원 슬릿 (one-slit) 이해/구현 했다
; 두개슬릿 (two-slit) 으로 결과는 얻어 물리학회에 투고해보자
3. 작은입자는 의식을 가지고 지 맘대로 움직이는거 같다.