티스토리 뷰
이제껏 일베의 수많은 정보글을 봐왔고, 그때마다 새로운 걸 배워왔지만 정작 나는 정보글을 투고한 적이 없더라고
그래서 나도 뭔가 게이들에게 정보를 알려주는 활동을 해야겠다!라고 생각해서 이 정보글을 써본다 이기야!
처음으로 쓰는 만큼 일베의 정보글 형식에 크게 벗어나도 이해해주길 바란다
자 잡담은 이쯤하고, 이제 본론으로 들어갈게. 내가 오늘 다룰 정보는 수학 관련 정보야
바로 음수와 음수를 곱하면 양수가 되는 이유를 알아보기 위해서이지
초딩 때 선생님으로부터 '음수×음수 = 양수' 라고 배운 적 있지?
그런데 분명 일게이들 중에서 이 공식에 관해 의아해한 적이 있을 거야
'왜 음수 곱하기 음수가 양수인가?' 라고 말야
양수 곱하기 양수는 똑같이 양수면서, 음수 곱하기 음수는 왜 정반대로 양수가 나올까??
다들 오랜시간 동안 이 사실은 '그저 그런가보다 ㅇㅇ'하고 아무런 증명없이 받아들이고 의구심없이 공식을 써먹었겠지만
이 사실을 알지 못하고 내키는대로 '음수×음수 = 음수'라고 생각해버리면 계산상의 큰 오류가 발생해
그래서 이 공식을 오늘 증명해보이려고 해
자 일단 이 공식을 증명하기 위한 두 종류의 방법을 보여줄게
우선 먼저 보여줄 방법은 간단하게 생각할 수 있는 논리적 전개이고, 다음에 보여줄 방법은 수학적 증명이야
1. 논리적 전개
자 이건 곱셈을 '수직선에서 나아가는 방향'과 '보는 방향'이라고 생각하면 쉬워
이게 무슨 말이냐면, 수직선위에서 사람이 서있고, 그 사람이 나아가는 방향과 보는 방향이라고 보면돼.
수직선에서 양수는 앞이라고 생각하고 음수는 뒤라고 생각하자
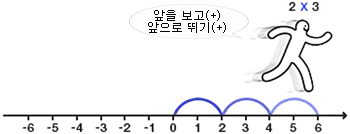
그러면 일단 '양수×양수'를 그림으로 표현하자면 이렇게 돼
즉, '양수×양수' 는 '앞을 보고 앞으로 뛴다'라고 생각할 수 있겠지?
앞을 보고 앞으로 뛴 결과는 양수이므로, '양수×양수 = 양수'라고 생각할 수 있어. (이건 당연한 사실)
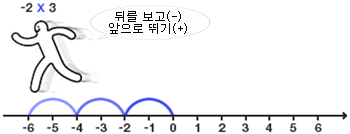
그렇다면 '음수×양수'나 '양수×음수'는 어떨까?
각각 이렇게 되겠지?
어라?! 근데 둘다 결과적으로 음수가 나왔네? 그러므로 '음수×양수'나 '양수×음수'는 둘다 음수라고 볼 수 있어 (이것 역시 당연한 사실)
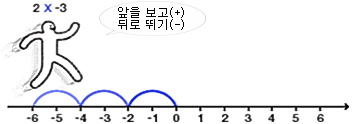
자 이젠 우리가 다루는 '음수×음수'에 대한 결과를 볼 차례야
이것도 위의 그림 대로 생각해보면 결과가 쉽게 나오겠지?
한번 해보자!
'음수×음수' 는 즉, '뒤를 보고 뒤로 뛰는 것'.. 그렇게 하니 '양수'가 나왔다
그러므로 '음수×음수 = 양수'이다.
2. 수학적 증명
사실, 위의 논리적 전개는 논리적으로 빈약한 점이 있어. '왜 양수를 앞이라고 생각해야하고 음수를 뒤라고 생각해야 하지?'라고 반문하면 반박할 여지가 없거든
그래서 중1 수학과정을 거친 사람이라면 누구나 이해할 수 있는 수학적인 증명을 해보이려고 해
일단 '음수×음수'에서 하나의 음수는 -x, 다른 하나는 -y라고 미지수로 놓자. 그러면
(-x) × (-y) 라고 표현할 수 있어.
(-x) × (-y) = (-x) × (-y) 라고 놓자. 이건 당연한 사실이지? 2 = 2 인것 처럼
(-x) × (-y) = (-x) × (-y) +0 뒤에 0을 더해도 값에는 아무런 영향을 줄 수 없지.
(-x) × (-y) = (-x) × (-y) +{(-xy) + xy } (-xy) + xy = 0 이야. 왜 인지는 알지? 그러므로 결과적으론 0이 더해진거나 마찬가지
(-x) × (-y) = {(-x) × (-y) +(-xy)} + xy 위의 식을 결합법칙으로 이렇게 만들어줬어.
(-x) × (-y) = (-x){(-y) +y} + xy 이것을 또 분배법칙을 이용해 (-x)로 묶어줬어. 어 그런데 (-y) +y = 0 이니까 (-x){(-y) +y}도 0이겠네?
(-x) × (-y) = 0+xy 0이 더해진 건 값에 변화가 없으므로 생략할 수 있다.
(-x) × (-y) = xy 그래서 이렇게 된다 이기야!
(-x) × (-y) = xy 가 뭘 의미하는 지 알겠지? '음수×음수 = 양수'를 수학적인 식으로 표현한거지.
자 이렇게 '음수×음수 = 양수'인 이유를 알아보았어.
어렸을 때부터 이 공식에 의문을 갖고 있던 게이들은 지금이라도 이를 통해 풀었으면 좋겠다!