티스토리 뷰
오늘도 할일없이 웹서핑을 하던 도중, 신박한 이미지들이 있어서 가져와봤다.
원을 굴려서 생긴 곡선들인데 긴말 말고 한번 보자.
이건 사이클로이드라는 곡선인데 원을 직선에다 굴렸을때 만들어지는 곡선이다.
이 곡선의 재밋는 점은 두 점을 잇는 낙하경로 중에 가장 빠른 경로라는거다.
50초 쯤부터 보면 되는데 자세히 보면 사이클로이드 경로가 자동차가 더 빨리 떨어진다.
다른 경로들도 무수히 많은데 왜 굳이 원을 굴려서 나오는 경로가 가장 시간이 적게 걸리는지 궁금하지 않노?
다음으로 이런 곡선도 있다.
커테이트 사이클로이드란다.
사이클로이드는 반지름길이 만큼 떨어져있는 점의 경로였는데
이 곡선의 경우 반지름보다 짧은 길이만큼 떨어져있는 점의 경로다.
사이클로이드에 비해 꼭지점이 무뎌진게 보이지? 과연 저 꼭지점은 무디게 보이는걸까 아니면 확대하면 사이클로이드처럼 뾰족할까?
반지름 길이보다 길게해서 굴릴수도 있다.
이제 한 단계 더 나아가서 직선위에서 원을 굴리는 것이 아니라
원 위에서 원을 굴리면 어떤 경로가 나올까?
정지한 원과 굴리는 원의 크기에 따라서 이런 여러가지 모양이 나온다.
원이 한번 돌아갈때마다 뾰족한 부분이 생기는게 보이지?
이런 뾰족한 부분을 커스프라고 하는데 위에 그림에서는 커스프가 각각 1, 2, 3, 4개인 경우다.
커스프가 한개인 곡선을 카디오이드(심장을 닮았다고 해서 그렇다네), 두개면 네프로이드라고 부른단다.
커스프가 다섯개인 경우는 이렇게 생겼는데
라넌쿨로이드라고 부른다고 하네. 이름이 야리꾸리한 감이 있는데 이러한 곡선들이 많이 쓰이기 때문에 이름이 붙은 것 아니겠노?
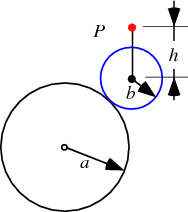
커테이트 사이클로이드때 처럼 반지름을 작게하거나, 아니면 크게해서 굴릴 수도 있는데 그러면 이런 모양이 된다.
이런 곡선을 에피트로코이드라고 부른단다. 전체적으로 ~오이드라고 부르는데 이게 아마 그리스어 라던가... 정확하지 않다.
원 밖에서 굴려봤으니 원 안에서도 굴려봐야하지 않겠노?
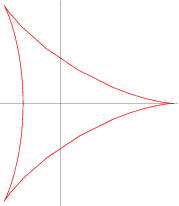
이 놈은 델토이드
이놈은 아스트로이드다.
이미지가 신박해서 가져왔는데 쓰고보니 별 메시지는 없노 ㅋㅋㅋ
잠깐 알아본 바로는 이런 것들을 기어 디자인에 쓸 수 있다고 하네. 기계공학하는 게이들한테는 중요하지 않겠노?
이런 식으로
그리고 사이클로이드를 가지고 진자를 만들 수도 있는데
이 진자는 주기가 진폭과 상관이 없단다.
무슨말이냐면 보통 진자는 줄이 길면 길수록 한번 왔다갔다 하는데 걸리는 시간이 길어지는데
사이클로이드 진자는 줄을 아무리 길게해도 왔다갔다 하는데 걸리는 시간은 일정하다는 얘기다.
신기하지?
세줄요약
1. 원을 굴리면
2. 재미있는 곡선이
3. 나온다.